Thank you for your interest in this topic.
The theory lies behind the LCAO method: the numerical atomic orbital (which is the zeta function you mentioned) is
a product of radial function and a spherical harmonic, which can be written as
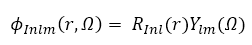
where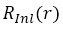 
is a numerical radial function, 
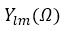is the spherical harmonic with angular variable .
The 1-dimensional radial function provided in the NanoDCAL basis sets is defined by data.OrbitalSet.rrData and data.OrbitalSet.frData (radial grid and values). If the basis is "single zeta" or SZ, the atomic orbital is exactly what it is. If "double zeta" or DZ, we essentially use two radial functions for each valence state. If SZP, we add one more "polarization orbital". Larger basis size normally gives better band results at higher energies, although it increases computation time.
If we plot the radial functions of Au (the MATLAB script is provided at the end of this dialogue):
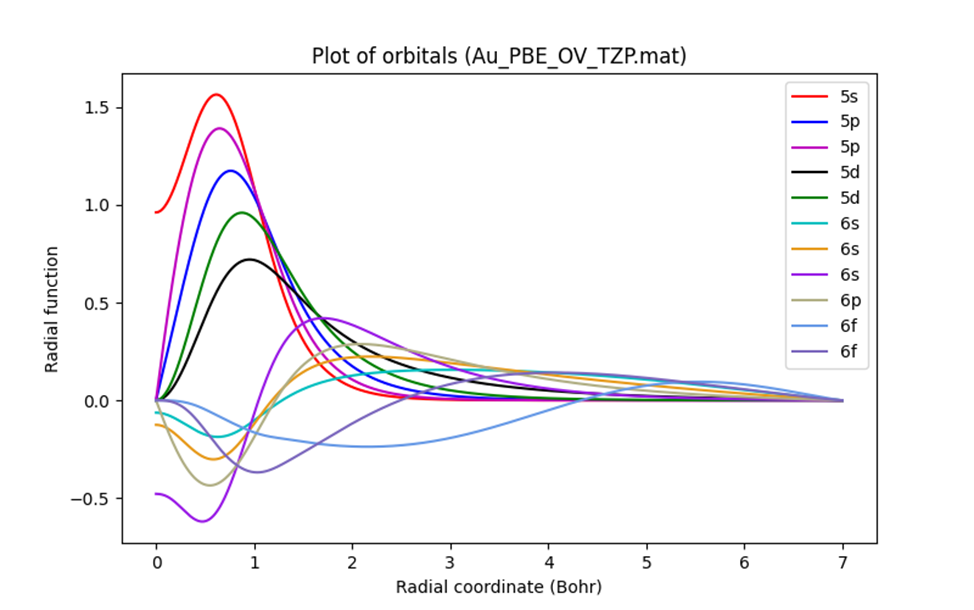
The 3-dimensional spherical harmonic (reference: https://www.osti.gov/servlets/purl/4370075) represents the angular part of the atomic orbital. In NanoDCAL, the spherical harmonics are calculated during the two-center integration process but are not saved as output.
If you want to compute the atomic orbital yourself, you need to multiply the 1-dimensional radial function by the 3-dimensional spherical harmonic to obtain the complete atomic orbital function for the specified quantum numbers.
If you have any question, please don't hesitate to contact us.
MATLAB scripts to plot the radial functions of a basis (you need to first load the basis in MATLAB):
function plotOrbitals(data)
% PLOTPSEUDOPOTENTIAL
figure
for ii = 1:length(data.OrbitalSet)
tmp = sprintf('L=%d',data.OrbitalSet(ii).Parameter.L);
dat = data.OrbitalSet(ii);
plot(dat.rrData,dat.frData,'LineWidth',2,'DisplayName',tmp); hold on
end
xlabel('Radial coordinate (Bohr)')
ylabel('Radial function')
legend()
